A calculator for arithmetic modulo N
Modular Arithmetic



What is it about?
A calculator for arithmetic modulo N. It lets you choose a fixed modulus, and then make lots of calculations without having to press a "mod" button again and again. It also:

App Screenshots




App Store Description
A calculator for arithmetic modulo N. It lets you choose a fixed modulus, and then make lots of calculations without having to press a "mod" button again and again. It also:
- follows the order convention;
- supports arbitrarily large numbers;
- performs fast modular division and exponentiation;
- can show a full transcript of your calculation.
Modular arithmetic is a "calculus of remainders". It features throughout mathematics and computer science, and has applications from cryptography to barcodes to music.
The basic idea is that you choose a modulus N, and then reduce every number to one of the integers 0,1,2,...,N−1 according to what remainder it leaves when dividing by N.
For example, using a modulus of 17:
40 ≡ 6 (since 40 ÷ 17 leaves a remainder of 6);
17 ≡ 0 (since 17 ÷ 17 leaves no remainder at all).
Arithmetic follows these same rules. Still using a modulus of 17:
15 + 7 ≡ 5 (since 22 ≡ 5);
3 × 9 ≡ 10 (since 27 ≡ 10);
5 ^ 3 ≡ 6 (since 125 ≡ 6).
Subtraction and division behave in a way that complements addition and multiplication:
−1 ≡ 16 (since 16 + 1 = 17 ≡ 0);
1/2 ≡ 9 (since 9 × 2 = 18 ≡ 1);
4 - 7 ≡ 14 (since 14 + 7 = 21 ≡ 4);
7 ÷ 3 = 8 (since 8 × 3 = 24 ≡ 7).
There are no negative numbers or fractions: like −1 and 7 ÷ 3 in the examples above, these are also reduced to one of 0,1,...,N−1.
As usual, you cannot divide by zero. You also cannot divide if the right hand side has any common factors with the modulus. If we change our modulus to 10, then the following operations all generate errors:
3 ÷ 20 (since 20 ≡ 0);
7 ÷ 8 (since 8 and 10 have a common factor of 2).
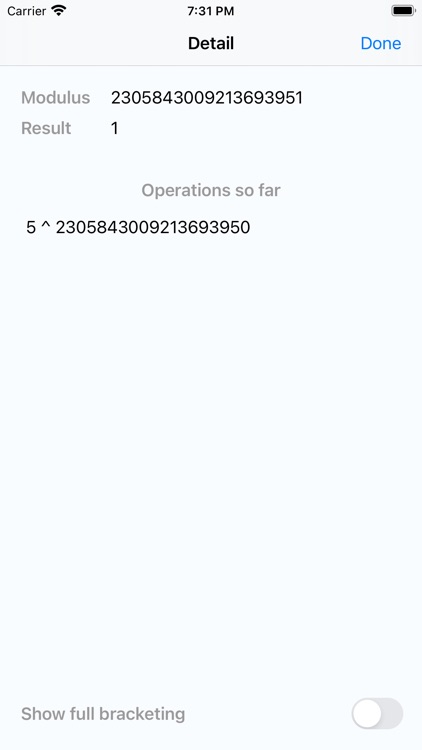
Integers can be arbitrarily large. For instance, if we set our modulus to 2305843009213693951 (a Mersenne prime), then:
5 ^ 2305843009213693950 ≡ 1 (by Fermat's little theorem).
The code is written carefully, and is backed up by a thorough suite of 186 automated tests.
This app supports external keyboards, Siri Shortcuts, and (on iPad) Slide Over, Split View, and multiple windows.
AppAdvice does not own this application and only provides images and links contained in the iTunes Search API, to help our users find the best apps to download. If you are the developer of this app and would like your information removed, please send a request to takedown@appadvice.com and your information will be removed.