
The Gauss-Krüger coordinate system is implemented as a generalized Transverse Mercator projection

Gauss Projector - Gauss-Kruger Projection
What is it about?
The Gauss-Krüger coordinate system is implemented as a generalized Transverse Mercator projection. This projection is similar to the Mercator except that the cylinder is longitudinal along a meridian instead of the equator. The result is a conformal projection that does not maintain true directions. The central meridian is placed on the region to be highlighted. This centering minimizes distortion of all properties in that region. This projection is best suited for land masses that stretch north–south. The Gauss–Krüger (GK) coordinate system is based on the Gauss–Krüger projection.

App Screenshots



App Store Description
The Gauss-Krüger coordinate system is implemented as a generalized Transverse Mercator projection. This projection is similar to the Mercator except that the cylinder is longitudinal along a meridian instead of the equator. The result is a conformal projection that does not maintain true directions. The central meridian is placed on the region to be highlighted. This centering minimizes distortion of all properties in that region. This projection is best suited for land masses that stretch north–south. The Gauss–Krüger (GK) coordinate system is based on the Gauss–Krüger projection.
Gauss–Krüger coordinate system. Gauss–Krüger divides the world into zones six degrees wide. Each zone has a scale factor of 1.0 and a false easting of 500,000 meters. The central meridian of zone 1 is at 3° E. Some places also add the zone number times one million to the 500,000 false easting value. GK zone 5 could have a false easting value of 500,000 or 5,500,000 meters. Three degree Gauss–Krüger zones exist also.
The UTM system is similar. The scale factor is 0.9996, and the central meridian of UTM zone 1 is at 177° W. The false easting value is 500,000 meters, and southern hemisphere zones also have a false northing of 10,000,000.
[Features]
1) support direct and inverse solution of Gauss-Krüger Projection.
2) support 3° and 6° zone-dividing.
3) support several types of reference ellipsoid.
4) support using GPS to get the location, and transform it to Gauss–Krüger coordinate.
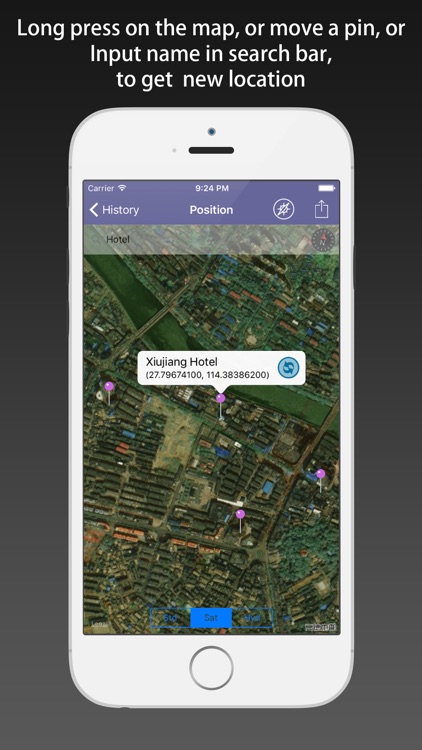
5) support moving the pin on the map to obtain the latitude and longitude of the location, and transform them.
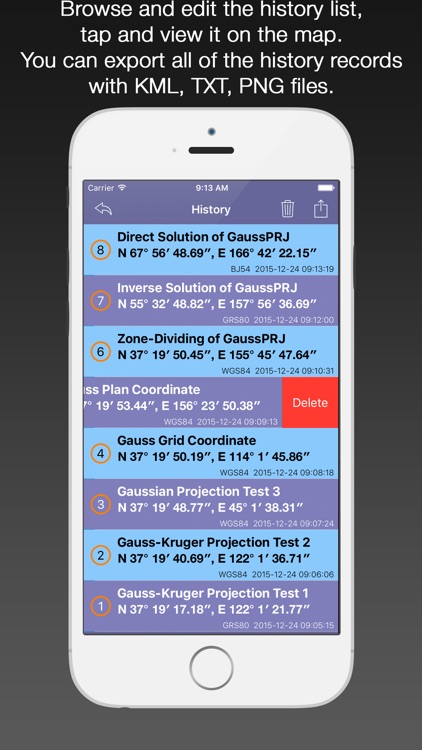
6) support saving the map projection results, and the history records can be viewed, deleted, cleaned up, and shared.
7) Every the historical record can be shown on the map, and each of them can be reduced again.
[Location Input Method]
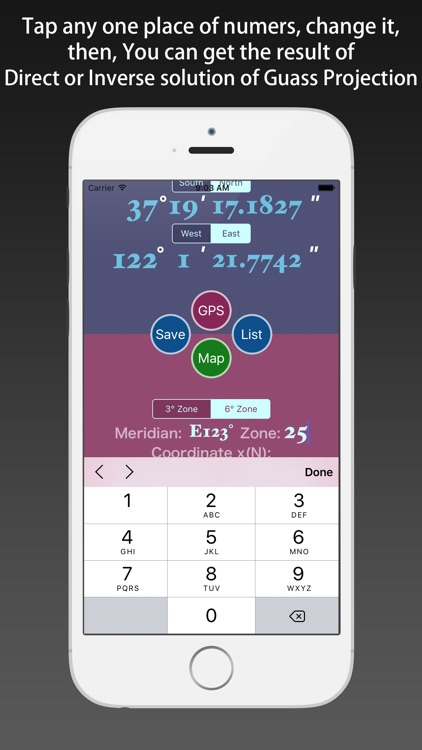
1) using the keyboard input by hand.
2) using the GPS positioning.
3) moving the pin on the map.
[Instructions]
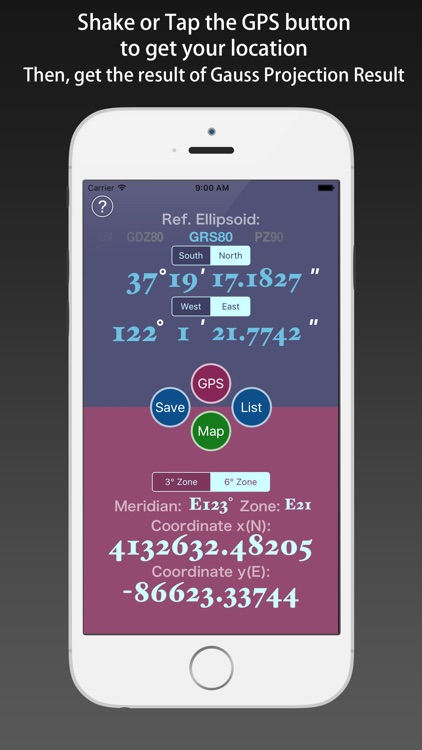
Direct solution of the Gauss Projection:
1) Select the Reference Ellipsoid.
2) Tap the “GPS” button to get the location.
3) Or Input the location using keyboard.
4) Inputed the number, tap the “Done” button, then you can get the Gauss Coordinate.
Inverse solution of the Gauss Projection:
1) Select the Reference Ellipsoid.
2) Input the zone number.
3) Input the Gauss Coordinate components (x, y).
4) Inputed the number, tap the “Done” button, then you can get the Geodetic Coordinate.
Warning: The App supports the Universal Gauss-Krüger coordinate (with false offset), based on the Natural Gauss-Krüger coordinate (no false offset). You can set the configurations for it in the “Setting / Help” view page. The corporate settings options will change the value of coordinate y (E) only.
“With Translation” means 500000 meters added on the natural coordinate y (E).
“With Zone Number” means “the zone number * 1000000” is added to the above value.
AppAdvice does not own this application and only provides images and links contained in the iTunes Search API, to help our users find the best apps to download. If you are the developer of this app and would like your information removed, please send a request to takedown@appadvice.com and your information will be removed.